| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 & 2 (Before Exercise 13.1) | Exercise 13.1 | Example 3 to 5 (Before Exercise 13.2) |
| Exercise 13.2 | ||
Chapter 13 Introduction to Graphs
Welcome to the solutions guide for Chapter 13, "Introduction to Graphs," from the latest Class 8 NCERT mathematics textbook designed for the academic session 2024-25. This chapter marks a pivotal transition in data representation, moving beyond the statistical graphs like bar graphs, histograms, and pie charts (primarily covered in Data Handling) towards the fundamental concepts of coordinate geometry and the versatile utility of line graphs. Understanding how to plot points and interpret graphs drawn on a coordinate plane is an essential skill for visualizing relationships between variables, analyzing trends, and forming a foundation for higher mathematics, particularly algebra and calculus. These solutions provide comprehensive, step-by-step assistance for all exercises, focusing on building both practical plotting skills and interpretive abilities.
The cornerstone of this chapter is the introduction to the Cartesian Coordinate System. This system provides a precise way to locate points on a flat surface (a plane) using two perpendicular number lines. The solutions clearly explain the key components:
- The horizontal number line, called the x-axis.
- The vertical number line, called the y-axis.
- The point where the x-axis and y-axis intersect, known as the Origin, denoted as $(0, 0)$.
A major focus of this chapter, extensively covered in the solutions, is the construction and interpretation of Line Graphs. These graphs are particularly effective for showing how a quantity changes continuously over time or for visualizing the relationship between two variables where data points are connected sequentially. The solutions demonstrate the systematic process of drawing line graphs from given data tables:
- Choosing appropriate scales for both the x-axis and y-axis to accommodate the range of data values effectively.
- Clearly labeling both axes, indicating the quantities they represent and the units used.
- Accurately plotting the data points corresponding to the given pairs of values.
- Connecting these points sequentially using line segments to form the graph.
Beyond construction, the ability to interpret existing line graphs is paramount. The solutions guide students on how to extract meaningful information from these visual representations. This includes reading the value of one variable corresponding to a specific value of the other, identifying periods of increase, decrease, or stability (horizontal segments), locating maximum or minimum values, and comparing different sections of the graph. Common examples explored include interpreting distance-time graphs (where the slope conceptually relates to speed, though formal slope calculation isn't the focus), temperature-time graphs, or graphs showing other relationships relevant to everyday life or simple experiments. The solutions help answer specific questions based solely on the graphical information presented.
Regarding the rationalized syllabus for 2024-25, Chapter 13, "Introduction to Graphs," in the Class 8 NCERT textbook has been streamlined to focus primarily on the basics of the coordinate system (plotting and reading points) and the construction and interpretation of line graphs based on given data. Sections explicitly dealing with plotting graphs of linear equations (e.g., plotting $y=2x+3$) and related concepts like identifying linear graphs from equations have been largely removed. The emphasis is on understanding graphical representation of data rather than graphing algebraic functions. By diligently working through these focused solutions, students can gain familiarity with the coordinate plane, master the practical skills of plotting points and drawing line graphs, develop crucial abilities in interpreting graphical data, and build a solid foundation for future work with graphs in mathematics and science.
Example 1 & 2 (Before Exercise 13.1)
Example 1: (A graph on “performance”)
The given graph (Fig 13.3) represents the total runs scored by two batsmen A and B, during each of the ten different matches in the year 2007. Study the graph and answer the following questions.

(i) What information is given on the two axes?
(ii) Which line shows the runs scored by batsman A?
(iii) Were the run scored by them same in any match in 2007? If so, in which match?
(iv) Among the two batsmen, who is steadier? How do you judge it?
Answer:
We analyze the given line graph to answer the questions.
(i) What information is given on the two axes?
The horizontal axis (or the x-axis) indicates the matches played during the year 2007.
The vertical axis (or the y-axis) shows the total runs scored in each match.
(ii) Which line shows the runs scored by batsman A?
Looking at the graph, there are two lines: a solid line and a dotted line. The graph legend indicates which line represents which batsman.
The dotted line shows the runs scored by Batsman A. (This is indicated at the top of the graph).
(iii) Were the run scored by them same in any match in 2007? If so, in which match?
To find if their runs were the same, we look for the point where the two lines intersect.
Observing the graph, the dotted line (Batsman A) and the solid line (Batsman B) meet at one point.
This intersection occurs during the 4th match. At this point, both batsmen have scored the same number of runs, which is 60 runs. (This is indicated by the point at which both graphs meet).
So, yes, their runs were the same in the 4th match.
(iv) Among the two batsmen, who is steadier? How do you judge it?
A steadier batsman is one whose performance is more consistent, showing less variation in scores from match to match.
Looking at the graph, Batsman A has one great "peak" (high score) but also many deep "valleys" (low scores, including two zeroes).
He does not appear to be consistent as his scores fluctuate a lot.
Batsman B, on the other hand, has never scored below a total of 40 runs, even though his highest score is only 100 in comparison to Batsman A's highest score of 115.
Also, Batsman A has scored a zero in two matches and in a total of 5 matches he has scored less than 40 runs.
Since Batsman A has a lot of ups and downs in his scores, Batsman B shows more consistency and reliability.
Therefore, Batsman B is the steadier batsman.
Example 2: The given graph (Fig 13.4) describes the distances of a car from a city P at different timeswhen it is travelling from City P to City Q, which are 350 km apart. Study the graph and answer the following:

(i) What information is given on the two axes?
(ii) From where and when did the car begin itsjourney?
(iii) How far did the car go in the first hour?
(iv) How far did the car go during (i) the 2nd hour? (ii) the 3rd hour?
(v) Was the speed same during the first three hours? How do you know it?
(vi) Did the car stop for some duration at any place? Justify your answer.
(vii) When did the car reach City Q?
Answer:
We analyse the given distance-time graph.
(i) What information is given on the two axes?
The horizontal (x) axis shows the time.
The vertical (y) axis shows the distance of the car from City P.
(ii) From where and when did the car begin its journey?
The car started from City P at 8 a.m.
(iii) How far did the car go in the first hour?
The first hour is from 8 a.m. to 9 a.m.
At 8 a.m. it just started from City P (distance 0 km).
At 9 a.m. it was at the 50th km (seen from graph).
Hence during the one-hour time between 8 a.m. and 9 a.m. the car travelled 50 km.
(iv) How far did the car go during (i) the 2nd hour? (ii) the 3rd hour?
The distance covered by the car during:
(a) the 2nd hour (i.e., from 9 am to 10 am) is 100 km, (calculated as $150 - 50$).
(b) the 3rd hour (i.e., from 10 am to 11 am) is 50 km (calculated as $200 - 150$).
(v) Was the speed same during the first three hours? How do you know it?
From the answers to questions (iii) and (iv), we find that the speed of the car was not the same all the time.
The graph illustrates how the speed varied by having segments with different slopes.
(vi) Did the car stop for some duration at any place? Justify your answer.
Yes, the car stopped for some duration.
We find that the car was 200 km away from city P when the time was 11 a.m. and also at 12 noon.
This shows that the car did not travel during the interval 11 a.m. to 12 noon.
The horizontal line segment representing “travel” during this period is illustrative of this fact.
(vii) When did the car reach City Q?
City Q is 350 km away from City P.
Looking at the graph, the car reaches the 350 km mark from City P at 2 p.m.
The car reached City Q at 2 p.m.
Exercise 13.1
Question 1. The following graph shows the temperature of a patient in a hospital, recorded every hour.
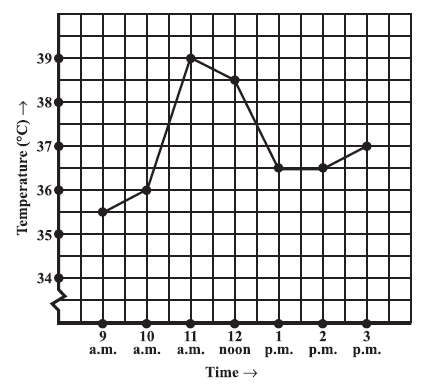
(a) What was the patient’s temperature at 1 p.m. ?
(b) When was the patient’s temperature 38.5° C?
(c) The patient’s temperature was the same two times during the period given. What were these two times?
(d) What was the temperature at 1.30 p.m.? How did you arrive at your answer?
(e) During which periods did the patients’ temperature showed an upward trend?
Answer:
We analyse the given line graph showing the patient's temperature.
(a) What was the patient’s temperature at 1 p.m. ?
The patient’s temperature at 1 p.m. was $36.5^\circ\text{C}$.
(b) When was the patient’s temperature $38.5^\circ\text{C}$?
The patient’s temperature was $38.5^\circ\text{C}$ at 12 noon.
(c) The patient’s temperature was the same two times during the period given. What were these two times?
The patient’s temperature was the same two times during the period given at 1 p.m. and 2 p.m.
(d) What was the temperature at 1.30 p.m.? How did you arrive at your answer?
The temperature at 1.30 p.m. was $36.5^\circ\text{C}$.
The point between 1 p.m. and 2 p.m. on the x-axis is equidistant from the two points showing 1 p.m. and 2 p.m., so it will represent 1.30 p.m. Similarly, the point on the y-axis, between $36^\circ\text{C}$ and $37^\circ\text{C}$ will represent $36.5^\circ\text{C}$. By looking at the graph at 1.30 p.m., the temperature is $36.5^\circ\text{C}$.
(e) During which periods did the patients’ temperature showed an upward trend?
The periods during which the patients’ temperature showed an upward trend are 9 a.m. to 10 a.m., 10 a.m. to 11 a.m., and 2 p.m. to 3 p.m.
Question 2. The following line graph shows the yearly sales figures for a manufacturing company.
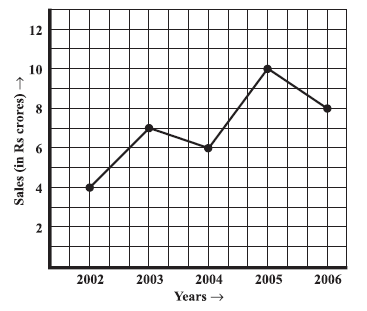
(a) What were the sales in (i) 2002 (ii) 2006?
(b) What were the sales in (i) 2003 (ii) 2005?
(c) Compute the difference between the sales in 2002 and 2006.
(d) In which year was there the greatest difference between the sales as compared to its previous year?
Answer:
Given:
The provided line graph illustrates the yearly sales figures (in $\textsf{₹}$ crores) achieved by a manufacturing company spanning the period from 2002 to 2006.
The horizontal axis (x-axis) represents the years, while the vertical axis (y-axis) shows the sales amount in $\textsf{₹}$ crores.
From the graph, we can interpret the sales for each year as follows:
Sales in 2002 = $\textsf{₹} 4$ crores
Sales in 2003 = $\textsf{₹} 7$ crores
Sales in 2004 = $\textsf{₹} 6$ crores
Sales in 2005 = $\textsf{₹} 10$ crores
Sales in 2006 = $\textsf{₹} 8$ crores
Solution:
(a) What were the sales in (i) 2002 (ii) 2006?
From the given information interpreted from the graph:
(i) Sales in 2002 were $\textsf{₹} 4$ crores.
(ii) Sales in 2006 were $\textsf{₹} 8$ crores.
(b) What were the sales in (i) 2003 (ii) 2005?
From the given information interpreted from the graph:
(i) Sales in 2003 were $\textsf{₹} 7$ crores.
(ii) Sales in 2005 were $\textsf{₹} 10$ crores.
(c) Compute the difference between the sales in 2002 and 2006.
Sales in 2006 = $\textsf{₹} 8$ crores
Sales in 2002 = $\textsf{₹} 4$ crores
Difference in sales = Sales in 2006 - Sales in 2002
$Difference = \textsf{₹} 8$ crores - $\textsf{₹} 4$ crores
$Difference = \textsf{₹} (8 - 4)$ crores
$Difference = \textsf{₹} 4$ crores.
(d) In which year was there the greatest difference between the sales as compared to its previous year?
We calculate the year-on-year difference in sales for each year starting from 2003.
Difference in sales in 2003 compared to 2002:
Sales in 2003 - Sales in 2002 = $\textsf{₹} (7 - 4)$ crores = $\textsf{₹} 3$ crores.
Difference in sales in 2004 compared to 2003:
Sales in 2004 - Sales in 2003 = $\textsf{₹} (6 - 7)$ crores = $\textsf{₹} -1$ crores.
Difference in sales in 2005 compared to 2004:
Sales in 2005 - Sales in 2004 = $\textsf{₹} (10 - 6)$ crores = $\textsf{₹} 4$ crores.
Difference in sales in 2006 compared to 2005:
Sales in 2006 - Sales in 2005 = $\textsf{₹} (8 - 10)$ crores = $\textsf{₹} -2$ crores.
The year-on-year differences in sales are $\textsf{₹} 3$ crores (2003), $\textsf{₹} -1$ crores (2004), $\textsf{₹} 4$ crores (2005), and $\textsf{₹} -2$ crores (2006).
We are looking for the greatest difference, which means the largest magnitude of change (either increase or decrease).
Magnitudes of the differences are: $|3| = 3$, $|-1| = 1$, $|4| = 4$, $|-2| = 2$.
Comparing the magnitudes ($3, 1, 4, 2$), the greatest difference is $\textsf{₹} 4$ crores.
This greatest difference occurred in the year 2005 (when sales increased by $\textsf{₹} 4$ crores compared to 2004).
Question 3. For an experiment in Botany, two different plants, plant A and plant B were grown under similar laboratory conditions. Their heights were measured at the end of each week for 3 weeks. The results are shown by the following graph.

(a) How high was Plant A after (i) 2 weeks (ii) 3 weeks?
(b) How high was Plant B after (i) 2 weeks (ii) 3 weeks?
(c) How much did Plant A grow during the 3rd week?
(d) How much did Plant B grow from the end of the 2nd week to the end of the 3rd week?
(e) During which week did Plant A grow most?
(f) During which week did Plant B grow least?
(g) Were the two plants of the same height during any week shown here? Specify.
Answer:
Given:
The provided line graph shows the heights (in cm) of two different plants, Plant A (dashed line) and Plant B (solid line), measured at the end of each week for 3 weeks, starting from Week 0.
From the graph, we can interpret the heights of the plants at the end of each week as follows:
Plant A:
End of Week 0: 0 cm
End of Week 1: 2 cm
End of Week 2: 7 cm
End of Week 3: 9 cm
Plant B:
End of Week 0: 0 cm
End of Week 1: 1 cm
End of Week 2: 7 cm
End of Week 3: 10 cm
Solution:
(a) How high was Plant A after (i) 2 weeks (ii) 3 weeks?
Reading from the given heights:
(i) After 2 weeks (at the end of Week 2), the height of Plant A was $\mathbf{7 \text{ cm}}$.
(ii) After 3 weeks (at the end of Week 3), the height of Plant A was $\mathbf{9 \text{ cm}}$.
(b) How high was Plant B after (i) 2 weeks (ii) 3 weeks?
Reading from the given heights:
(i) After 2 weeks (at the end of Week 2), the height of Plant B was $\mathbf{7 \text{ cm}}$.
(ii) After 3 weeks (at the end of Week 3), the height of Plant B was $\mathbf{10 \text{ cm}}$.
(c) How much did Plant A grow during the 3rd week?
Growth during the 3rd week = Height at the end of Week 3 - Height at the end of Week 2 (for Plant A)
$Growth = 9 \text{ cm} - 7 \text{ cm}$
$Growth = \mathbf{2 \text{ cm}}$.
Plant A grew by $\mathbf{2 \text{ cm}}$ during the 3rd week.
(d) How much did Plant B grow from the end of the 2nd week to the end of the 3rd week?
This is the growth of Plant B during the 3rd week.
Growth during the 3rd week = Height at the end of Week 3 - Height at the end of Week 2 (for Plant B)
$Growth = 10 \text{ cm} - 7 \text{ cm}$
$Growth = \mathbf{3 \text{ cm}}$.
Plant B grew by $\mathbf{3 \text{ cm}}$ from the end of the 2nd week to the end of the 3rd week.
(e) During which week did Plant A grow most?
Let's calculate the growth of Plant A during each week:
Growth during 1st week = Height at end of Week 1 - Height at end of Week 0 = $2 \text{ cm} - 0 \text{ cm} = 2 \text{ cm}$.
Growth during 2nd week = Height at end of Week 2 - Height at end of Week 1 = $7 \text{ cm} - 2 \text{ cm} = 5 \text{ cm}$.
Growth during 3rd week = Height at end of Week 3 - Height at end of Week 2 = $9 \text{ cm} - 7 \text{ cm} = 2 \text{ cm}$.
Comparing the growth in each week (2 cm, 5 cm, 2 cm), the greatest growth for Plant A was $\mathbf{5 \text{ cm}}$ during the 2nd week.
(f) During which week did Plant B grow least?
Let's calculate the growth of Plant B during each week:
Growth during 1st week = Height at end of Week 1 - Height at end of Week 0 = $1 \text{ cm} - 0 \text{ cm} = 1 \text{ cm}$.
Growth during 2nd week = Height at end of Week 2 - Height at end of Week 1 = $7 \text{ cm} - 1 \text{ cm} = 6 \text{ cm}$.
Growth during 3rd week = Height at end of Week 3 - Height at end of Week 2 = $10 \text{ cm} - 7 \text{ cm} = 3 \text{ cm}$.
Comparing the growth in each week (1 cm, 6 cm, 3 cm), the least growth for Plant B was $\mathbf{1 \text{ cm}}$ during the 1st week.
(g) Were the two plants of the same height during any week shown here? Specify.
Looking at the given heights at the end of each week:
End of Week 0: Plant A = 0 cm, Plant B = 0 cm. Yes, they were the same height.
End of Week 1: Plant A = 2 cm, Plant B = 1 cm. Not the same height.
End of Week 2: Plant A = 7 cm, Plant B = 7 cm. Yes, they were the same height.
End of Week 3: Plant A = 9 cm, Plant B = 10 cm. Not the same height.
Based on the data provided, the two plants were of the same height at the end of Week 0 (0 cm) and at the end of Week 2 (7 cm).
Question 4. The following graph shows the temperature forecast and the actual temperature for each day of a week.

(a) On which days was the forecast temperature the same as the actual temperature?
(b) What was the maximum forecast temperature during the week?
(c) What was the minimum actual temperature during the week?
(d) On which day did the actual temperature differ the most from the forecast temperature?
Answer:
Given:
The provided line graph displays the temperature forecast (dotted line) and the actual temperature (solid line) for each day of a week.
The horizontal axis represents the days of the week, and the vertical axis represents the temperature in degrees Celsius ($^\circ\text{C}$).
From the graph, we can interpret the temperatures for each day as follows:
Monday: Forecast = $15^\circ\text{C}$, Actual = $17.5^\circ\text{C}$
Tuesday: Forecast = $20^\circ\text{C}$, Actual = $20^\circ\text{C}$
Wednesday: Forecast = $25^\circ\text{C}$, Actual = $30^\circ\text{C}$
Thursday: Forecast = $22.5^\circ\text{C}$, Actual = $15^\circ\text{C}$
Friday: Forecast = $15^\circ\text{C}$, Actual = $15^\circ\text{C}$
Saturday: Forecast = $30^\circ\text{C}$, Actual = $25^\circ\text{C}$
Sunday: Forecast = $35^\circ\text{C}$, Actual = $35^\circ\text{C}$
Solution:
(a) On which days was the forecast temperature the same as the actual temperature?
We compare the forecast and actual temperatures for each day:
Monday: $15^\circ\text{C} \neq 17.5^\circ\text{C}$ (Not same)
Tuesday: $20^\circ\text{C} = 20^\circ\text{C}$ (Same)
Wednesday: $25^\circ\text{C} \neq 30^\circ\text{C}$ (Not same)
Thursday: $22.5^\circ\text{C} \neq 15^\circ\text{C}$ (Not same)
Friday: $15^\circ\text{C} = 15^\circ\text{C}$ (Same)
Saturday: $30^\circ\text{C} \neq 25^\circ\text{C}$ (Not same)
Sunday: $35^\circ\text{C} = 35^\circ\text{C}$ (Same)
The forecast temperature was the same as the actual temperature on Tuesday, Friday, and Sunday.
(b) What was the maximum forecast temperature during the week?
We look at the forecast temperatures for each day: $15^\circ\text{C}, 20^\circ\text{C}, 25^\circ\text{C}, 22.5^\circ\text{C}, 15^\circ\text{C}, 30^\circ\text{C}, 35^\circ\text{C}$.
The maximum value among these temperatures is $35^\circ\text{C}$.
The maximum forecast temperature during the week was $\mathbf{35^\circ\text{C}}$.
(c) What was the minimum actual temperature during the week?
We look at the actual temperatures for each day: $17.5^\circ\text{C}, 20^\circ\text{C}, 30^\circ\text{C}, 15^\circ\text{C}, 15^\circ\text{C}, 25^\circ\text{C}, 35^\circ\text{C}$.
The minimum value among these temperatures is $15^\circ\text{C}$.
The minimum actual temperature during the week was $\mathbf{15^\circ\text{C}}$.
(d) On which day did the actual temperature differ the most from the forecast temperature?
We calculate the absolute difference between the forecast and actual temperature for each day:
Monday: $|15 - 17.5| = |-2.5| = 2.5^\circ\text{C}$
Tuesday: $|20 - 20| = 0^\circ\text{C}$
Wednesday: $|25 - 30| = |-5| = 5^\circ\text{C}$
Thursday: $|22.5 - 15| = 7.5^\circ\text{C}$
Friday: $|15 - 15| = 0^\circ\text{C}$
Saturday: $|30 - 25| = 5^\circ\text{C}$
Sunday: $|35 - 35| = 0^\circ\text{C}$
Comparing the differences ($2.5^\circ\text{C}, 0^\circ\text{C}, 5^\circ\text{C}, 7.5^\circ\text{C}, 0^\circ\text{C}, 5^\circ\text{C}, 0^\circ\text{C}$), the greatest difference is $7.5^\circ\text{C}$.
This greatest difference occurred on Thursday.
Question 5. Use the tables below to draw linear graphs.
(a) The number of days a hill side city received snow in different years.
| Year | 2003 | 2004 | 2005 | 2006 |
|---|---|---|---|---|
| Days | 8 | 10 | 5 | 12 |
(b) Population (in thousands) of men and women in a village in different years.
| Year | 2003 | 2004 | 2005 | 2006 | 2007 |
|---|---|---|---|---|---|
| Number of Men | 12 | 12.5 | 13 | 13.2 | 13.5 |
| Number of WoMen | 11.3 | 11.9 | 13 | 13.6 | 12.8 |
Answer:
Given:
Two tables are provided, containing data on the number of days a hillside city received snow over different years and the population of men and women in a village over different years.
Solution:
To draw a linear graph from the given tables, we will plot the data points as coordinates (x, y) on a graph paper and then join these points with line segments.
(a) Snowfall data
We take 'Year' on the horizontal axis (x-axis) and 'Number of Days' on the vertical axis (y-axis).
The points to be plotted are:
For 2003, Days = 8 $\implies (2003, 8)$
For 2004, Days = 10 $\implies (2004, 10)$
For 2005, Days = 5 $\implies (2005, 5)$
For 2006, Days = 12 $\implies (2006, 12)$
Steps to draw the graph:
1. Draw two perpendicular axes on a graph paper. Label the horizontal axis as 'Year' and the vertical axis as 'Number of Days'.
2. Choose a suitable scale for both axes. For the x-axis, years are discrete points, so mark them as 2003, 2004, 2005, 2006 at equal intervals. For the y-axis, a scale like 1 unit = 2 days would be appropriate to accommodate the values from 5 to 12.
3. Plot the points $(2003, 8)$, $(2004, 10)$, $(2005, 5)$, and $(2006, 12)$ on the graph.
4. Join the plotted points with straight line segments in order (from 2003 to 2004, 2004 to 2005, and 2005 to 2006) to get the linear graph.
(b) Population data
We will draw two separate lines on the same graph, one for the number of men and one for the number of women.
Take 'Year' on the horizontal axis (x-axis) and 'Population (in thousands)' on the vertical axis (y-axis).
The points to be plotted for the Number of Men line are:
For 2003, Men = 12 thousand $\implies (2003, 12)$
For 2004, Men = 12.5 thousand $\implies (2004, 12.5)$
For 2005, Men = 13 thousand $\implies (2005, 13)$
For 2006, Men = 13.2 thousand $\implies (2006, 13.2)$
For 2007, Men = 13.5 thousand $\implies (2007, 13.5)$
The points to be plotted for the Number of Women line are:
For 2003, Women = 11.3 thousand $\implies (2003, 11.3)$
For 2004, Women = 11.9 thousand $\implies (2004, 11.9)$
For 2005, Women = 13 thousand $\implies (2005, 13)$
For 2006, Women = 13.6 thousand $\implies (2006, 13.6)$
For 2007, Women = 12.8 thousand $\implies (2007, 12.8)$
Steps to draw the graph:
1. Draw two perpendicular axes on a graph paper. Label the horizontal axis as 'Year' and the vertical axis as 'Population (in thousands)'.
2. Choose a suitable scale for both axes. For the x-axis, mark the years 2003, 2004, 2005, 2006, 2007 at equal intervals. For the y-axis, the values range from 11.3 to 13.6, so a scale like 1 unit = 0.5 thousand would be appropriate. You may start the vertical axis from a value slightly below the minimum data point (e.g., 11) to make the variations clearer.
3. Plot the points for the Number of Men line: $(2003, 12)$, $(2004, 12.5)$, $(2005, 13)$, $(2006, 13.2)$, and $(2007, 13.5)$. Join these points with straight line segments. You can use a specific colour or line style (e.g., solid line) for this line.
4. Plot the points for the Number of Women line: $(2003, 11.3)$, $(2004, 11.9)$, $(2005, 13)$, $(2006, 13.6)$, and $(2007, 12.8)$. Join these points with straight line segments. Use a different colour or line style (e.g., dashed line) for this line.
5. Add a legend to indicate which line represents the number of men and which represents the number of women.
Question 6. A courier-person cycles from a town to a neighbouring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown by the following graph.

(a) What is the scale taken for the time axis?
(b) How much time did the person take for the travel?
(c) How far is the place of the merchant from the town?
(d) Did the person stop on his way? Explain.
(e) During which period did he ride fastest?
Answer:
Given:
The provided line graph shows the distance of a courier-person from a town at different times as he cycles to a suburban area to deliver a parcel to a merchant.
The horizontal axis represents the time in hours, and the vertical axis represents the distance from the town in km.
From the graph, we can interpret the distance from the town at different times:
At 8:00 am: Distance = 0 km
At 9:00 am: Distance = 10 km (Distance travelled: $10 - 0 = 10$ km)
At 10:00 am: Distance = 16 km (Distance travelled: $16 - 10 = 6$ km)
At 10:30 am: Distance = 16 km (Distance travelled: $16 - 16 = 0$ km - Stopped)
At 11:30 am: Distance = 22 km (Distance travelled: $22 - 16 = 6$ km)
The journey to the merchant's place (reaching the destination at 22 km) was completed by 11:30 am as shown in the graph.
Solution:
(a) What is the scale taken for the time axis?
On the time axis (horizontal axis), the interval between 8:00 am and 9:00 am represents 1 hour. This interval is divided into 4 smaller units (blocks).
So, 4 units on the time axis represent 1 hour.
The scale taken for the time axis is $\mathbf{4 \text{ units} = 1 \text{ hour}}$.
(b) How much time did the person take for the travel?
The journey starts at 8:00 am. According to the given information, the journey to the merchant's place (reaching 22 km from the town) was completed by 11:30 am.
Total time taken for travel = End time - Start time
Total time taken = 11:30 am - 8:00 am
Total time taken = $\mathbf{3 \text{ hours} 30 \text{ minutes}}$.
This can also be written as $3.5$ hours or $3\frac{1}{2}$ hours.
(c) How far is the place of the merchant from the town?
The graph shows the courier reaches a distance of 22 km from the town at 11:30 am (as per the given information) and the distance remains constant after that. This indicates that the merchant's place is located at this distance.
The place of the merchant is $\mathbf{22 \text{ km}}$ far from the town.
(d) Did the person stop on his way? Explain.
Yes, the person stopped on his way.
A horizontal line segment in a distance-time graph indicates that the distance from the starting point is not changing, which means the person is stationary (stopped) during that time.
From the graph, there is a horizontal segment from 10:00 am to 10:30 am. During this period, the distance from the town remains constant at 16 km.
This indicates that the person stopped for $\mathbf{30 \text{ minutes}}$ between 10:00 am and 10:30 am.
(e) During which period did he ride fastest?
The speed is the distance covered per unit of time. In a distance-time graph, speed is represented by the slope of the line segment. A steeper slope indicates a higher speed.
Let's calculate the speed during each moving interval based on the given points:
1. Period from 8:00 am to 9:00 am:
Distance covered = $10 \text{ km} - 0 \text{ km} = 10 \text{ km}$.
Time taken = 9:00 am - 8:00 am = 1 hour.
Speed = $\frac{\text{Distance}}{\text{Time}} = \frac{10 \text{ km}}{1 \text{ hour}} = 10 \text{ km/hr}$.
2. Period from 9:00 am to 10:00 am:
Distance covered = $16 \text{ km} - 10 \text{ km} = 6 \text{ km}$.
Time taken = 10:00 am - 9:00 am = 1 hour.
Speed = $\frac{6 \text{ km}}{1 \text{ hour}} = 6 \text{ km/hr}$.
3. Period from 10:30 am to 11:30 am:
Distance covered = $22 \text{ km} - 16 \text{ km} = 6 \text{ km}$.
Time taken = 11:30 am - 10:30 am = 1 hour.
Speed = $\frac{6 \text{ km}}{1 \text{ hour}} = 6 \text{ km/hr}$.
Comparing the speeds during the moving intervals (10 km/hr, 6 km/hr, 6 km/hr), the fastest speed is 10 km/hr.
The person rode fastest during the period from $\mathbf{8:00 \text{ am}}$ to $\mathbf{9:00 \text{ am}}$.
Question 7. Can there be a time-temperature graph as follows? Justify your answer.

Answer:
We need to examine each of the four graphs provided and determine if they can represent a valid time-temperature relationship.
Graph (i)
This graph shows that as time increases, the temperature is increasing. For any given time, there is only one corresponding temperature value. This is physically possible (e.g., heating a substance).
Yes, this can be a time-temperature graph.
Graph (ii)
This graph shows that as time increases, the temperature is decreasing. For any given time, there is only one corresponding temperature value. This is physically possible (e.g., cooling a substance).
Yes, this can be a time-temperature graph.
Graph (iii)
This graph shows that at a certain point in time (where the vertical line occurs), there are multiple different temperature values. A physical object or system can only have one temperature at any given instant in time. A vertical line on a time-temperature graph implies an instantaneous change across a range of temperatures at a fixed time, which is not possible in reality.
No, this cannot be a time-temperature graph.
Graph (iv)
This graph shows a horizontal line.
A horizontal line on this graph means that as time progresses (moving along the horizontal axis), the value on the vertical axis (Temperature) remains constant.
It is possible for the temperature to remain constant over a period of time. For example, if something is being heated at a constant rate and is undergoing a phase change (like water boiling at $100^\circ\text{C}$), or if the surrounding temperature is stable.
Therefore, a graph with a horizontal line can be a time-temperature graph, representing a period where the temperature did not change.
Yes, this can be a time-temperature graph.
Example 3 to 5 (Before Exercise 13.2)
Example 3: (Quantity and Cost)
The following table gives the quantity of petrol and its cost.
| No. of Litres of petrol | 10 | 15 | 20 | 25 |
|---|---|---|---|---|
| Cost of petrol in ₹ | 500 | 750 | 1000 | 1250 |
Plot a graph to show the data.
Answer:
Given:
A table showing the number of litres of petrol and their corresponding cost in $\textsf{₹}$.
Solution:
The given data shows the relationship between the quantity of petrol and its cost. As the quantity of petrol increases, the cost also increases. Let's check if it's a linear relationship by calculating the cost per litre:
For 10 litres: $\frac{500}{10} = \textsf{₹} 50$ per litre.
For 15 litres: $\frac{750}{15} = \textsf{₹} 50$ per litre.
For 20 litres: $\frac{1000}{20} = \textsf{₹} 50$ per litre.
For 25 litres: $\frac{1250}{25} = \textsf{₹} 50$ per litre.
Since the cost per litre is constant ($\textsf{₹} 50$), the relationship between the quantity of petrol and its cost is directly proportional and linear.
We will plot a linear graph to represent this data.
Let the Number of Litres of petrol be represented on the horizontal axis (x-axis).
Let the Cost of petrol in $\textsf{₹}$ be represented on the vertical axis (y-axis).
From the table, the data points can be written as ordered pairs (Number of Litres, Cost):
(10, 500)
(15, 750)
(20, 1000)
(25, 1250)
To plot the graph:
1. Draw two perpendicular lines (axes) on a graph paper. The horizontal line is the x-axis and the vertical line is the y-axis.
2. Mark the intersection of the axes as the origin (0,0).
3. Label the x-axis as 'Number of Litres of petrol' and the y-axis as 'Cost in $\textsf{₹}$'.
4. Choose a suitable scale for each axis. For the x-axis, you can take 1 unit to represent 5 litres. For the y-axis, you can take 1 unit to represent $\textsf{₹}$ 250.
5. Plot the points corresponding to the ordered pairs (10, 500), (15, 750), (20, 1000), and (25, 1250).
6. Join the plotted points with a straight line. Since the cost is directly proportional to the quantity, the graph should be a straight line passing through the origin.
Example 4: (Principal and Simple Interest)
A bank gives 10% Simple Interest (S.I.) on deposits by senior citizens. Draw a graph to illustrate the relation between the sum deposited and simple interest earned. Find from your graph
(a) the annual interest obtainable for an investment of ₹ 250.
(b) the investment one has to make to get an annual simple interest of ₹ 70
Answer:
Given:
A bank gives 10% Simple Interest (S.I.) per annum on deposits by senior citizens.
Solution:
The relationship between Simple Interest (S.I.), Principal (P), Rate (R), and Time (T) is given by the formula:
$\text{S.I.} = \frac{P \times R \times T}{100}$
In this case, the rate (R) is 10% per annum, and we are looking for annual interest, so the time (T) is 1 year.
The formula simplifies to:
$\text{S.I.} = \frac{P \times 10 \times 1}{100} = \frac{10P}{100} = \frac{P}{10}$
This shows that the Simple Interest is directly proportional to the Principal amount deposited. This relationship is linear.
To draw the graph, we need some data points (Principal, S.I.). We can choose a few values for the Principal and calculate the corresponding Simple Interest.
Let Principal be on the horizontal axis (x-axis) and Simple Interest be on the vertical axis (y-axis).
| Principal P ($\textsf{₹}$) | Simple Interest S.I. ($\textsf{₹}$) ($S.I. = \frac{P}{10}$) | Point (P, S.I.) |
| 0 | $\frac{0}{10} = 0$ | (0, 0) |
| 100 | $\frac{100}{10} = 10$ | (100, 10) |
| 200 | $\frac{200}{10} = 20$ | (200, 20) |
| 500 | $\frac{500}{10} = 50$ | (500, 50) |
| 1000 | $\frac{1000}{10} = 100$ | (1000, 100) |
Steps to draw the graph:
1. Draw two perpendicular axes on a graph paper. Label the horizontal axis as 'Principal (in $\textsf{₹}$)' and the vertical axis as 'Simple Interest (in $\textsf{₹}$)'.
2. Mark the intersection of the axes as the origin (0,0).
3. Choose suitable scales for both axes. For the horizontal axis (Principal), a scale of 1 unit = $\textsf{₹}$ 100 would be appropriate. For the vertical axis (Simple Interest), a scale of 1 unit = $\textsf{₹}$ 10 would be appropriate.
4. Plot the points from the table: (0, 0), (100, 10), (200, 20), (500, 50), (1000, 100).
5. Since the relationship is linear, draw a straight line passing through the origin (0,0) and connecting these plotted points.
Now we use the graph to answer the questions:
(a) the annual interest obtainable for an investment of $\textsf{₹}$ 250.
To find the interest for an investment of $\textsf{₹}$ 250, locate 250 on the Principal axis (horizontal axis). 250 is halfway between 200 and 300 on the chosen scale.
Move vertically up from $\textsf{₹}$ 250 on the horizontal axis to intersect the graph line.
From the intersection point on the line, move horizontally left to the Simple Interest axis (vertical axis).
Read the value on the vertical axis. This value should be 25.
The annual interest obtainable for an investment of $\textsf{₹}$ 250 is $\textsf{₹}$ 25.
(b) the investment one has to make to get an annual simple interest of $\textsf{₹}$ 70
To find the investment needed to get an interest of $\textsf{₹}$ 70, locate 70 on the Simple Interest axis (vertical axis). Assuming a scale of 1 unit = $\textsf{₹}$ 10, 70 would be at the $70/10 = 7$ unit mark.
Move horizontally right from $\textsf{₹}$ 70 on the vertical axis to intersect the graph line.
From the intersection point on the line, move vertically down to the Principal axis (horizontal axis).
Read the value on the horizontal axis. This value should be 700.
The investment one has to make to get an annual simple interest of $\textsf{₹}$ 70 is $\textsf{₹}$ 700.
Example 5: (Time and Distance)
Ajit can ride a scooter constantly at a speed of 30 kms/hour. Draw a time-distance graph for this situation. Use it to find
(i) the time taken by Ajit to ride 75 km.
(ii) the distance covered by Ajit in $3\frac{1}{2}$ hours.
Answer:
Given:
Ajit rides a scooter at a constant speed of 30 km/hour.
Solution:
The speed of Ajit is constant at 30 km/hour. The relationship between distance (D), speed (S), and time (T) is $D = S \times T$.
In this case, $S = 30$ km/h. So, the relationship is $D = 30T$.
This is a linear relationship, so the graph will be a straight line passing through the origin (since at Time = 0, Distance = 0).
To draw the time-distance graph, we need some data points (Time, Distance). We can choose a few values for Time and calculate the corresponding Distance using the formula $D = 30T$.
Let Time (in hours) be on the horizontal axis (x-axis) and Distance (in km) be on the vertical axis (y-axis).
| Time T (hours) | Distance D (km) ($D = 30T$) | Point (T, D) |
| 0 | $30 \times 0 = 0$ | (0, 0) |
| 1 | $30 \times 1 = 30$ | (1, 30) |
| 2 | $30 \times 2 = 60$ | (2, 60) |
| 3 | $30 \times 3 = 90$ | (3, 90) |
| 4 | $30 \times 4 = 120$ | (4, 120) |
Steps to draw the graph:
1. Draw two perpendicular axes on a graph paper. Label the horizontal axis as 'Time (in hours)' and the vertical axis as 'Distance (in km)'.
2. Mark the intersection of the axes as the origin (0,0).
3. Choose suitable scales for both axes. For the horizontal axis (Time), you can take 1 unit to represent 1 hour. For the vertical axis (Distance), you can take 1 unit to represent 10 km or 15 km (e.g., 1 unit = 15 km would accommodate values up to 120 easily).
4. Plot the points from the table: (0, 0), (1, 30), (2, 60), (3, 90), (4, 120).
5. Since the speed is constant, the relationship is linear. Draw a straight line passing through the origin (0,0) and connecting these plotted points. Extend the line as needed to cover the required range for parts (i) and (ii).
Now we use the graph to answer the questions:
(i) the time taken by Ajit to ride 75 km.
To find the time taken for 75 km, locate 75 km on the Distance axis (vertical axis). Assuming a scale of 1 unit = 15 km, 75 km would be at the $75/15 = 5$ unit mark.
Move horizontally from 75 on the vertical axis to intersect the graph line.
From the intersection point on the line, move vertically down to the Time axis (horizontal axis).
Read the value on the horizontal axis. This value should be 2.5 (or $2\frac{1}{2}$).
The time taken by Ajit to ride 75 km is 2.5 hours (or $2\frac{1}{2}$ hours).
(ii) the distance covered by Ajit in $3\frac{1}{2}$ hours.
$3\frac{1}{2}$ hours is equal to 3.5 hours.
To find the distance covered in 3.5 hours, locate 3.5 on the Time axis (horizontal axis). Assuming a scale of 1 unit = 1 hour, 3.5 hours would be halfway between the 3 and 4 hour marks.
Move vertically up from 3.5 on the horizontal axis to intersect the graph line.
From the intersection point on the line, move horizontally left to the Distance axis (vertical axis).
Read the value on the vertical axis. This value should be 105.
The distance covered by Ajit in $3\frac{1}{2}$ hours is 105 km.
Exercise 13.2
Question 1. Draw the graphs for the following tables of values, with suitable scales on the axes.
(a) Cost of apples
| Number of apples | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Cost (in ₹) | 5 | 10 | 15 | 20 | 25 |
(b) Distance travelled by a car
| Time (in hours) | 6 a.m. | 7 a.m. | 8 a.m. | 9 a.m. |
|---|---|---|---|---|
| Distance (in km) | 40 | 80 | 120 | 160 |
(i) How much distance did the car cover during the period 7.30 a.m. to 8 a.m?
(ii) What was the time when the car had covered a distance of 100 km since it’s start?
(c) Interest on deposits for a year.
| Deposit (in ₹) | 1000 | 2000 | 3000 | 4000 | 5000 |
|---|---|---|---|---|---|
| Simple Interest (in ₹) | 80 | 160 | 240 | 320 | 400 |
(i) Does the graph pass through the origin?
(ii) Use the graph to find the interest on 2500 for a year.
(iii) To get an interest of 280 per year, how much money should be deposited?
Answer:
Given:
Three tables containing data relating Quantity and Cost (apples), Time and Distance (car), and Deposit and Simple Interest.
Solution:
We will draw a separate linear graph for each table as requested.
(a) Cost of apples
We need to plot the number of apples on the horizontal axis (x-axis) and the cost (in $\textsf{₹}$) on the vertical axis (y-axis).
The data points from the table are:
(1, 5), (2, 10), (3, 15), (4, 20), (5, 25)
Steps to draw the graph:
1. Draw two perpendicular axes (x-axis and y-axis) on a graph paper. Mark their intersection as the origin (0,0).
2. Label the x-axis as 'Number of Apples' and the y-axis as 'Cost (in $\textsf{₹}$)'.
3. Choose suitable scales. For the x-axis, 1 unit = 1 apple is a convenient scale. For the y-axis, 1 unit = $\textsf{₹}$ 5 is a suitable scale to accommodate the values.
4. Plot the points corresponding to the ordered pairs (1, 5), (2, 10), (3, 15), (4, 20), and (5, 25) on the graph.
5. Join the plotted points with a straight line. Since the cost is directly proportional to the number of apples (each apple costs $\textsf{₹}$ 5), the graph is a straight line passing through the origin (if you buy 0 apples, the cost is $\textsf{₹}$ 0, so (0,0) is also a point on the line).
(b) Distance travelled by a car
We need to plot Time (in hours) on the horizontal axis (x-axis) and Distance (in km) on the vertical axis (y-axis).
The data points from the table can be written as ordered pairs (Time, Distance):
(6 a.m., 40 km), (7 a.m., 80 km), (8 a.m., 120 km), (9 a.m., 160 km)
Steps to draw the graph:
1. Draw two perpendicular axes. Label the horizontal axis as 'Time' and the vertical axis as 'Distance (in km)'.
2. Mark the origin (0,0). Note that the car starts at 6 a.m. and has already covered some distance before the times given in the table are recorded. The graph starts at (6 a.m., 40 km).
3. Choose suitable scales. For the horizontal axis, let the distance between the markings for consecutive hours represent 1 hour. For the vertical axis, a scale of 1 unit = 20 km or 40 km would work. Let's use 1 unit = 40 km.
4. Plot the points (6 a.m., 40), (7 a.m., 80), (8 a.m., 120), and (9 a.m., 160).
5. Join the plotted points with a straight line. Since the increase in distance is constant for each hour (40 km per hour), the car travels at a constant speed, so the graph is a straight line.
Now answer the questions based on the graph:
(i) How much distance did the car cover during the period 7.30 a.m. to 8 a.m?
From the graph (or the table), at 7 a.m., the distance from the start is 80 km. At 8 a.m., the distance from the start is 120 km. The time period is from 7 a.m. to 8 a.m., which is 1 hour. The distance covered during this hour is $120 \text{ km} - 80 \text{ km} = 40 \text{ km}$.
The period 7.30 a.m. to 8 a.m. is a duration of 30 minutes, which is half of an hour.
Assuming the car maintains its constant speed of 40 km/hour, the distance covered in 30 minutes will be half of the distance covered in 1 hour.
Distance covered in 30 minutes = $\frac{1}{2} \times 40 \text{ km} = \mathbf{20 \text{ km}}$.
(ii) What was the time when the car had covered a distance of 100 km since it’s start?
We need to find the time when the distance from the starting point was 100 km.
From the graph, locate 100 km on the vertical axis (Distance).
Move horizontally from 100 km to the graph line.
From the intersection point, move vertically down to the horizontal axis (Time).
The value on the time axis corresponding to 100 km is halfway between 7 a.m. (80 km) and 8 a.m. (120 km). Halfway between 7 a.m. and 8 a.m. is 7:30 a.m.
The time when the car had covered a distance of 100 km since its start was 7:30 a.m.
(c) Interest on deposits for a year
We need to plot Deposit (Principal) on the horizontal axis (x-axis) and Simple Interest (in $\textsf{₹}$) on the vertical axis (y-axis).
The data points from the table are:
(1000, 80), (2000, 160), (3000, 240), (4000, 320), (5000, 400)
Let's first check the interest rate. Simple Interest (S.I.) = $\frac{\text{Principal} \times \text{Rate} \times \text{Time}}{100}$. For 1 year, $\text{S.I.} = \frac{\text{Principal} \times \text{Rate}}{100}$.
From the table, for Deposit $\textsf{₹}$ 1000, S.I. = $\textsf{₹}$ 80.
$80 = \frac{1000 \times \text{Rate}}{100}$
$80 = 10 \times \text{Rate}$
Rate = $\frac{80}{10} = 8\%$.
The simple interest is 8% per year. The relationship is $\text{S.I.} = 0.08 \times \text{Deposit}$, which is linear.
Steps to draw the graph:
1. Draw two perpendicular axes. Label the horizontal axis as 'Deposit (in $\textsf{₹}$)' and the vertical axis as 'Simple Interest (in $\textsf{₹}$)'.
2. Mark the intersection of the axes as the origin (0,0).
3. Choose suitable scales. For the horizontal axis (Deposit), a scale of 1 unit = $\textsf{₹}$ 1000 is appropriate. For the vertical axis (Simple Interest), a scale of 1 unit = $\textsf{₹}$ 80 is appropriate.
4. Plot the points corresponding to the ordered pairs (1000, 80), (2000, 160), (3000, 240), (4000, 320), and (5000, 400) on the graph.
5. Join the plotted points with a straight line. Since the Simple Interest is directly proportional to the Deposit, the graph is a straight line passing through the origin (if Deposit is $\textsf{₹}$ 0, S.I. is $\textsf{₹}$ 0, so (0,0) is also a point on the line).
Now answer the questions based on the graph:
(i) Does the graph pass through the origin?
Yes, the graph passes through the origin (0,0).
Explanation: If the deposit amount is $\textsf{₹}$ 0, the simple interest earned will also be $\textsf{₹}$ 0. So, the point (0, 0) lies on the graph.
(ii) Use the graph to find the interest on $\textsf{₹}$ 2500 for a year.
Locate $\textsf{₹}$ 2500 on the horizontal axis (Deposit). This value is exactly halfway between 2000 and 3000 on the horizontal axis.
Move vertically up from $\textsf{₹}$ 2500 on the horizontal axis to intersect the graph line.
From the point of intersection on the line, move horizontally left to the vertical axis (Simple Interest).
On the vertical axis, the value halfway between $\textsf{₹}$ 160 (corresponding to 2000) and $\textsf{₹}$ 240 (corresponding to 3000) is $\frac{160+240}{2} = \frac{400}{2} = \textsf{₹} 200$.
The interest on $\textsf{₹}$ 2500 for a year is $\textsf{₹}$ 200.
(iii) To get an interest of $\textsf{₹}$ 280 per year, how much money should be deposited?
Locate $\textsf{₹}$ 280 on the vertical axis (Simple Interest).
Move horizontally right from $\textsf{₹}$ 280 on the vertical axis to intersect the graph line.
From the point of intersection on the line, move vertically down to the horizontal axis (Deposit).
On the vertical axis, $\textsf{₹}$ 280 is exactly halfway between $\textsf{₹}$ 240 (corresponding to 3000 deposit) and $\textsf{₹}$ 320 (corresponding to 4000 deposit).
On the horizontal axis, the corresponding value should be halfway between $\textsf{₹}$ 3000 and $\textsf{₹}$ 4000, which is $\frac{3000+4000}{2} = \frac{7000}{2} = \textsf{₹} 3500$.
To get an interest of $\textsf{₹}$ 280 per year, $\textsf{₹}$ 3500 should be deposited.
Question 2. Draw a graph for the following.
(i)
| Side of square (in cm) | 2 | 3 | 3.5 | 5 | 6 |
|---|---|---|---|---|---|
| Perimeter (in cm) | 8 | 12 | 14 | 20 | 24 |
Is it a linear graph?
(ii)
| Side of square (in cm) | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Perimeter (in cm2) | 4 | 9 | 16 | 25 | 36 |
Is it a linear graph?
Answer:
Given:
Two tables are provided. Table (i) shows the relationship between the side length of a square and its perimeter. Table (ii) shows the relationship between the side length of a square and its area.
Solution:
We will draw a graph for each table and determine if it is a linear graph.
(i) Side of square vs. Perimeter
We need to plot the Side of square (in cm) on the horizontal axis (x-axis) and the Perimeter (in cm) on the vertical axis (y-axis).
The data points from the table are:
(2, 8), (3, 12), (3.5, 14), (5, 20), (6, 24)
Steps to draw the graph:
1. Draw two perpendicular axes (x-axis and y-axis) on a graph paper. Mark their intersection as the origin (0,0).
2. Label the x-axis as 'Side of square (in cm)' and the y-axis as 'Perimeter (in cm)'.
3. Choose suitable scales. For the x-axis, you can take 1 unit = 1 cm. For the y-axis, you can take 1 unit = 4 cm or 5 cm. Let's use 1 unit = 4 cm.
4. Plot the points corresponding to the ordered pairs (2, 8), (3, 12), (3.5, 14), (5, 20), and (6, 24) on the graph.
5. Join the plotted points with a straight line.
Is it a linear graph?
Yes, it is a linear graph.
Justification:
The perimeter of a square is calculated by the formula: Perimeter = $4 \times \text{Side}$. If we denote the side by $s$ and the perimeter by $P$, the relationship is $P = 4s$. This is a linear equation of the form $y = mx$, where $y=P$, $x=s$, and the slope $m=4$. When the points from the table are plotted and joined, they lie on a straight line that passes through the origin (because when the side length is 0, the perimeter is 0, so the point (0,0) is on the graph).
(ii) Side of square vs. Area
We need to plot the Side of square (in cm) on the horizontal axis (x-axis) and the Area (in cm$^2$) on the vertical axis (y-axis).
The data points from the table are:
(2, 4), (3, 9), (4, 16), (5, 25), (6, 36)
Steps to draw the graph:
1. Draw two perpendicular axes (x-axis and y-axis) on a graph paper. Mark their intersection as the origin (0,0).
2. Label the x-axis as 'Side of square (in cm)' and the y-axis as 'Area (in cm$^2$)'.
3. Choose suitable scales. For the x-axis, you can take 1 unit = 1 cm. For the y-axis, since the area values increase more rapidly (4, 9, 16, 25, 36), a scale like 1 unit = 5 cm$^2$ or 1 unit = 10 cm$^2$ would be more appropriate. Let's use 1 unit = 5 cm$^2$.
4. Plot the points corresponding to the ordered pairs (2, 4), (3, 9), (4, 16), (5, 25), and (6, 36) on the graph.
5. Join the plotted points. You will observe that the points do not lie on a single straight line.
Is it a linear graph?
No, it is not a linear graph.
Justification:
The area of a square is calculated by the formula: Area = $\text{Side} \times \text{Side}$ or $\text{Side}^2$. If we denote the side by $s$ and the area by $A$, the relationship is $A = s^2$. This is a quadratic relationship ($y = x^2$), not a linear one. When the points from the table are plotted, they will form a curve (specifically, part of a parabola), not a straight line.

